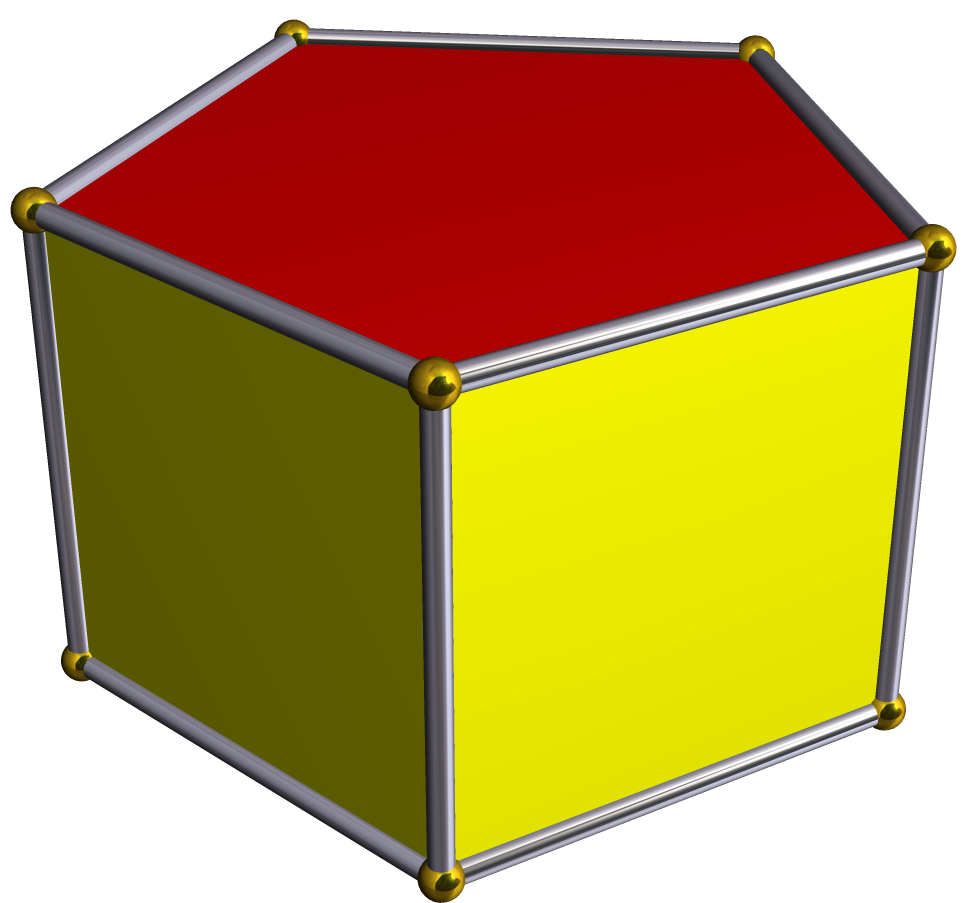
П’ятикутна призма стоїть перед нами як витончена конструкція, де прості лінії перетворюються на складну тривимірну форму, що захоплює уяву математиків і дизайнерів. Ця фігура, побудована на основі п’ятикутника, не просто абстрактний об’єкт з підручників геометрії – вона ховає в собі точні розрахунки, які визначають її структуру. Розглядаючи її ближче, ми бачимо, як дві паралельні основи з’єднуються бічними стінками, створюючи щось схоже на витягнутий кристал, що грає світлом у різних кутах.
У світі стереометрії призми займають особливе місце, бо вони ілюструють перехід від плоских фігур до об’ємних тіл. П’ятикутна версія, з її нерівномірними сторонами, додає шарму непередбачуваності, на відміну від симетричних кубів чи пірамід. Коли ми говоримо про грані, то маємо на увазі ті поверхні, що обмежують фігуру, і саме вони роблять призму такою впізнаваною.
Визначення п’ятикутної призми в геометрії
Призма як геометричне тіло виникає, коли ми беремо плоский багатокутник і “витягуємо” його вздовж прямої лінії, створюючи паралельні копії основи. Для п’ятикутної призми основою служить п’ятикутник – фігура з п’ятьма сторонами, яка може бути правильною, з рівними кутами, або неправильною, з різними довжинами ребер. Бічні грані формуються паралелограмами, що з’єднують відповідні вершини основ, і саме ця конструкція забезпечує стабільність форми.
Уявіть, як п’ятикутник, намальований на папері, раптом піднімається в просторі, ніби оживає під впливом невидимої сили. Ця трансформація не випадкова: математично призма визначається як многогранник з двома паралельними основами і бічними гранями, перпендикулярними до них у випадку прямій призми. Якщо ж бічні ребра нахилені, ми маємо справу з похилою версією, де грані перетворюються на трапеції, додаючи динаміки загальній структурі.
Історично призми вивчалися ще в античні часи, коли Евклід у своїх “Елементах” описував подібні фігури, хоча п’ятикутні варіанти набули популярності пізніше, з розвитком оптики та архітектури. Сьогодні, у 2025 році, з появою 3D-моделювання, ці фігури моделюються в програмах на кшталт Blender, де їхні властивості розраховуються з точністю до міліметра.
Кількість граней: основний розрахунок
Тепер перейдімо до серцевини питання – скільки ж граней у п’ятикутної призми. Відповідь криється в простій формулі: для будь-якої призми з n-кутною основою кількість граней дорівнює n + 2. Для п’ятикутника n = 5, тож загалом 7 граней: дві п’ятикутні основи і п’ять прямокутних або паралелограмних бічних граней.
Ця цифра не просто число – вона відображає баланс між основою і висотою. Кожна бічна грань відповідає одній стороні п’ятикутника, створюючи замкнуту оболонку, що утримує об’єм. Якщо призма правильна, з рівними сторонами, її грані ідеально симетричні, ніби вирізані з кришталю, але в реальних моделях, як у архітектурних макетах, вони можуть варіюватися, додаючи унікальності.
Щоб переконатися в точності, звернімося до авторитетних джерел: енциклопедичні видання, такі як uk.wikipedia.org, підтверджують, що п’ятикутна призма має саме 7 граней. Це узгоджується з математичними текстами, де формула застосовується універсально для всіх призм, незалежно від форми основи.
Детальний розбір кожної грані
Дві основи – це п’ятикутники, паралельні одна одній, ніби дзеркальні відображення в просторі. Вони визначають “обличчя” призми, і в правильній версії кожен кут дорівнює 108 градусам, створюючи гармонійну зірку в основі. Бічні грані, п’ять за числом, з’єднують їх, і в прямій призмі вони є прямокутниками, що стоять вертикально, наче стіни старовинного замку.
Коли призма похила, бічні грані набувають форми паралелограмів, з нахиленими кутами, що додає руху статичній фігурі. Кожна грань має свою площу, яку можна розрахувати: для основи – формула для п’ятикутника (5/4 * сторона² * cot(π/5)), а для бічних – просто добуток висоти на довжину сторони основи. Ці розрахунки не тільки теоретичні; вони застосовуються в інженерії, наприклад, при проектуванні оптичних призм для телескопів.
Ребер і вершин: повна картина структури
Грані – це лише частина історії; ребер у п’ятикутної призми 15, бо кожна основа має 5 ребер, плюс 5 вертикальних, що з’єднують їх. Вершин – 10, по 5 на кожній основі, ніби точки, що тримають всю конструкцію разом. Ці елементи пов’язані формулою Ейлера для многогранників: V – E + F = 2, де V=10, E=15, F=7, і справді, 10 – 15 + 7 = 2, підтверджуючи опуклість фігури.
Уявіть, як ці ребра переплітаються, створюючи каркас, подібний до молекулярної моделі. У правильній призмі всі ребра рівні, але в неправильній варіації довжини варіюються, що впливає на стабільність. Це особливо помітно в освітніх моделях, де школярі збирають призми з паличок, відчуваючи на дотик, як кожне ребро додає міцності.
Згідно з математичними ресурсами, такими як сайти на кшталт mathros.net.ua, ці числа незмінні для стандартної п’ятикутної призми, і будь-які відхилення вказують на іншу фігуру, як антипризму.
Формули для розрахунку елементів
Щоб глибше зануритися, розгляньмо загальні формули. Кількість граней F = n + 2, ребер E = 3n, вершин V = 2n, де n=5 для нашої призми. Ці рівняння не просто абстракції – вони дозволяють моделювати фігури в комп’ютерних програмах, прогнозуючи поведінку в реальних умовах, як у фізиці оптики.
Наприклад, об’єм V = площа основи * висота, а поверхня – сума площ усіх граней. Якщо основа правильний п’ятикутник зі стороною a, площа основи ≈ 1.72 a², і так далі. Ці деталі роблять призму інструментом для інженерів, які розраховують матеріали для конструкцій.
Типи п’ятикутних призм і їх особливості
П’ятикутні призми бувають прямими, де бічні ребра перпендикулярні основам, і похилими, з нахиленими ребрами. Правильна пряма призма має всі грані правильними багатокутниками, створюючи ідеальну симетрію, наче коштовний камінь. Похила версія, навпаки, нагадує скошену вежу, де грані витягуються під кутом, змінюючи оптичні властивості.
Є також оптичні призми, як пентапризма в фотоапаратах, де п’ятикутна форма відбиває світло на 90 градусів, забезпечуючи чітке зображення. У 2025 році, з розвитком VR-технологій, такі призми інтегруються в окуляри, покращуючи імерсію. Кожний тип впливає на кількість граней – завжди 7, але форма граней варіюється, додаючи нюансів.
- Пряма призма: Бічні грані – прямокутники, ідеальна для базових розрахунків, як у шкільній геометрії.
- Похила призма: Грані – паралелограми, корисна в архітектурі для створення динамічних форм, наприклад, в сучасних будівлях з нахиленими стінами.
- Оптична пентапризма: Спеціалізована версія з дзеркальними гранями, що використовується в техніці для корекції зображень, де точність кута відбиття критична.
Ці варіанти показують, як базова структура адаптується до потреб, від освіти до високих технологій. Переходячи до прикладів, ми бачимо, як теорія оживає в повсякденності.
Практичні приклади та застосування в житті
П’ятикутні призми не обмежуються теорією; вони з’являються в архітектурі, як у формі дахів деяких будівель, де п’ятикутна основа забезпечує стійкість. У природі подібні форми видно в кристалах, наприклад, в апатиті, де молекулярна структура імітує призму. У дизайні, як у ювелірних виробах, призматичні форми додають блиску, відбиваючи світло в несподіваних напрямках.
У сучасному світі, станом на 2025 рік, 3D-друк дозволяє створювати моделі п’ятикутних призм для освітніх цілей, де студенти можуть торкатися граней і рахувати їх вручну. У геймдизайні, в іграх на кшталт Minecraft, гравці будують подібні структури, навчаючись геометрії через гру. Ці приклади роблять абстрактну фігуру близькою, ніби частиною нашого щоденного оточення.
| Тип призми | Кількість граней | Застосування |
|---|---|---|
| Пряма правильна | 7 | Освітні моделі, базові конструкції |
| Похила | 7 | Архітектура, динамічні дизайни |
| Оптична | 7 | Фототехніка, телескопи |
Ця таблиця ілюструє універсальність, базуючись на даних з геометричних ресурсів. Джерело: сайти на кшталт reporter.zp.ua.
Цікаві факти про п’ятикутні призми
🧊 Чи знали ви, що пентапризма в фотоапаратах перевертає зображення, роблячи його правильним для ока, і це відкриття датується 19 століттям? У математиці п’ятикутні призми пов’язані з золотим перетином, бо правильний п’ятикутник має пропорції φ = (1 + √5)/2.
🔍 Ще один факт: у кристалографії існує понад 200 мінералів з призматичними формами, і деякі імітують п’ятикутні структури через молекулярні решітки. У поп-культурі, в фільмах на кшталт “Інтерстеллар”, призматичні форми символізують багатовимірність простору. 😎
Ці деталі додають шарму, показуючи, як геометрія переплітається з наукою і мистецтвом.
Математичні властивості та розрахунки
Глибше занурюючись, розгляньмо поверхневу площу: S = 2 * площа п’ятикутника + 5 * (сторона * висота). Для правильної основи площа п’ятикутника = (5/4) a² / tan(36°), де a – сторона. Об’єм простий: V = площа основи * h, і ці формули дозволяють прогнозувати поведінку в фізиці, як розсіювання світла.
У координатній геометрії вершини можна задати: наприклад, нижня основа в площині z=0 з координатами (cos(2πk/5), sin(2πk/5), 0) для k=0..4, верхня – з z=h. Це не тільки теорія; в програмуванні, як у Python з бібліотекою Matplotlib, такі моделі візуалізуються, допомагаючи студентам бачити грані в динаміці.
Емоційно кажучи, ці розрахунки викликають захват, бо перетворюють холодні числа на живу форму, ніби оживають сторінки підручника. Якщо ви колись моделювали призму, то знаєте, як кожна грань додає глибини сприйняттю.
Історичний контекст і еволюція вивчення
Призми вивчалися з часів Архімеда, але п’ятикутні набули уваги в епоху Відродження, коли Леонардо да Вінчі малював многогранники. У 17 столітті Кеплер використовував призматичні форми для моделювання планет, а сьогодні, у 2025, з AI, ми симулюємо складні призми для квантових обчислень.
Ця еволюція показує, як проста фігура з 7 гранями стала основою для інновацій, від оптики Ньютона до сучасних лазерів. У школах призми вчать як місток між 2D і 3D, розвиваючи просторове мислення.
Порівняння з іншими призмами
Порівняно з трикутною призмою (5 граней), п’ятикутна має більше складності, з 7 гранями, що робить її стабільнішою для певних конструкцій. Чотирикутна (6 граней) простіша, але п’ятикутна додає естетики, як у дизайні меблів. Шестикутна (8 граней) ще складніша, але всі вони слідують тій самій логіці n+2.
- Трикутна: 5 граней, проста для базових уроків.
- Чотирикутна: 6 граней, як коробка, практична в повсякденні.
- П’ятикутна: 7 граней, баланс між складністю і красою.
Це порівняння підкреслює унікальність нашої фігури, роблячи її вибором для креативних проектів.
Потенціал у майбутніх технологіях
У 2025 році п’ятикутні призми інтегруються в нанотехнології, де їхня форма оптимізує потік енергії в мікрочіпах. У екології вони надихають на енергоефективні будівлі, з дахами, що імітують призматичні грані для кращого освітлення. Майбутнє обіцяє ще більше, з VR-моделями, де ви можете “прогулятися” всередині призми, рахуючи грані наживо.
Ця перспектива надихає, бо показує, як давня геометрія стає частиною завтрашнього дня, з’єднуючи минуле з інноваціями.