Що таке правильний шестикутник і чому він особливий
Правильний шестикутник — це багатогранник із шістьма рівними сторонами та шістьма рівними кутами. Його краса полягає в ідеальній симетрії: кожна сторона має однакову довжину, а кожен кут — однакову міру. Ця геометрична досконалість робить шестикутник не лише естетично привабливим, але й надзвичайно корисним у природі, архітектурі та математиці. Наприклад, бджолині стільники мають форму шестикутників, адже це оптимальна форма для економії простору та матеріалів.
Щоб зрозуміти, чому дорівнює внутрішній кут правильного шестикутника, потрібно зануритися в геометричні основи. Внутрішній кут — це кут між двома сусідніми сторонами всередині фігури. Для правильного шестикутника всі внутрішні кути однакові, що спрощує наші розрахунки. Давайте крок за кроком розберемо, як знайти цю величину.
Формула для внутрішнього кута правильного багатогранника
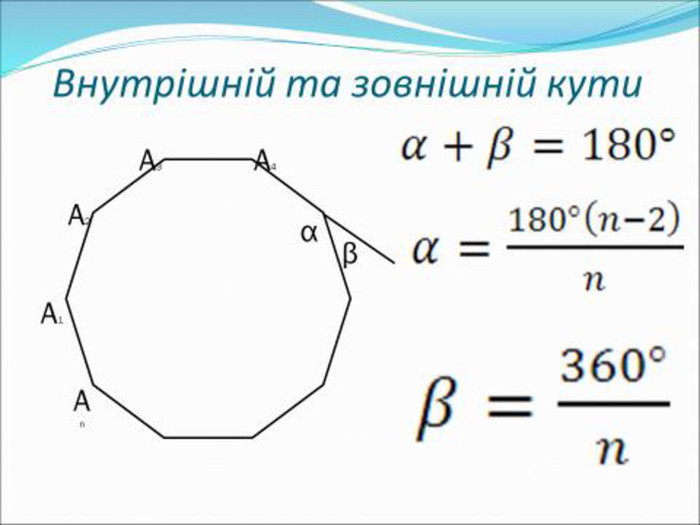
Для будь-якого правильного багатогранника (полігона) існує універсальна формула, яка допомагає знайти міру внутрішнього кута. Вона виглядає так: (n-2) × 180° / n, де n — кількість сторін фігури. Чому саме так? Давайте розберемо це детально, адже розуміння формули — ключ до розв’язання задачі.
- Крок 1: Сума внутрішніх кутів. Для будь-якого багатогранника сума всіх внутрішніх кутів дорівнює (n-2) × 180°. Це пов’язано з тим, що будь-який полігон можна розбити на (n-2) трикутники, а сума кутів у кожному трикутнику становить 180°.
- Крок 2: Розподіл на кожен кут. Оскільки правильний багатогранник має однакові кути, ми ділимо загальну суму кутів на кількість сторін (n), щоб знайти міру одного внутрішнього кута.
- Застосування до шестикутника. У шестикутника n = 6. Підставимо це значення у формулу: (6-2) × 180° / 6 = 4 × 180° / 6 = 720° / 6 = 120°. Отже, кожен внутрішній кут правильного шестикутника дорівнює 120°.
Ця формула — справжній математичний скарб, адже вона працює для будь-якого правильного багатогранника, від трикутника до додекагона. Для шестикутника результат завжди буде 120°, і це підтверджується як розрахунками, так і геометричними побудовами. Джерело: «Геометрія» Погорєлова О.В.
Чому внутрішній кут шестикутника саме 120°: геометричне пояснення
Розрахунок — це чудово, але давайте подивимося на шестикутник очима геометра. Уявіть ідеальний шестикутник, вписаний у коло. Кожна вершина шестикутника лежить на колі, а сторони — це хорди. Така конструкція називається правильним шестикутником, вписаним у коло, і вона дає нам ще один спосіб перевірити величину кутів.
Центр кола з’єднуємо з кожною вершиною шестикутника. Оскільки вершин шість, коло ділиться на шість рівних секторів, кожен із яких має центральний кут 360° / 6 = 60°. Тепер розглянемо трикутник, утворений центром кола та двома сусідніми вершинами шестикутника. Це рівнобедрений трикутник, де два кути при основі (біля вершин шестикутника) однакові.
Щоб знайти внутрішній кут шестикутника, нам потрібно врахувати, що сума кутів у трикутнику дорівнює 180°. У нашому рівнобедреному трикутнику центральний кут становить 60°, а два кути при основі — по (180° – 60°) / 2 = 60°. Але внутрішній кут шестикутника формується двома такими трикутниками, що сходяться у вершині. Таким чином, внутрішній кут дорівнює 60° + 60° = 120°. Цей підхід підтверджує наш попередній розрахунок і показує, як гармонійно працює геометрія!
Порівняння внутрішніх кутів різних правильних багатогранників
Щоб краще зрозуміти, чому 120° для шестикутника — це логічно, давайте порівняємо внутрішні кути різних правильних багатогранників. Така таблиця допоможе побачити закономірність і оцінити унікальність шестикутника.
| Багатогранник | Кількість сторін | Внутрішній кут |
|---|---|---|
| Трикутник | 3 | 60° |
| Чотирикутник | 4 | 90° |
| П’ятикутник | 5 | 108° |
| Шестикутник | 6 | 120° |
| Восьмикутник | 8 | 135° |
Джерело: «Основи геометрії» Кисельова А.П.
З таблиці видно, що зі збільшенням кількості сторін внутрішній кут зростає. Шестикутник із його 120° займає золоту середину: він більший, ніж у трикутника чи чотирикутника, але менший, ніж у восьмикутника. Ця властивість робить шестикутник ідеальним для мозаїк, адже три шестикутники, що сходяться у вершині, утворюють повний кут 360° (120° × 3 = 360°).
Цікаві факти про шестикутники 😊
Шестикутники — це не просто математична цікавинка, вони всюди навколо нас! Ось кілька захопливих фактів, які зроблять вас фанатом цієї форми:
- Бджолині стільники. Бджоли будують свої стільники у формі шестикутників, адже це найефективніший спосіб заповнити простір без зазорів, використовуючи мінімум воску.
- У природі. Шестикутні візерунки можна знайти в базальтових стовпах, як-от у Гігантській дорозі в Ірландії, де лава застигла у вигляді ідеальних шестикутних колон.
- У технологіях. Шестикутні сітки використовуються в архітектурі та дизайні, адже вони міцні й естетичні. Наприклад, сучасні будівлі часто мають фасади з шестикутними елементами.
- У математиці. Правильний шестикутник — єдиний багатогранник, який може повністю заповнити площину без зазорів разом із самим собою (так звана шестикутна мозаїка).
Ці факти показують, що шестикутник — не просто геометрична фігура, а справжній феномен, який поєднує математику, природу та мистецтво. Його внутрішній кут у 120° відіграє ключову роль у цій гармонії.
Як перевірити внутрішній кут шестикутника на практиці
Теорія — це чудово, але як переконатися, що внутрішній кут дійсно дорівнює 120°? Ось кілька практичних способів, які підійдуть як для учнів, так і для ентузіастів геометрії.
- Побудова шестикутника за допомогою циркуля. Намалюйте коло, виберіть точку на колі та відкладіть шість відрізків, рівних радіусу, вздовж кола. З’єднайте точки — і ось ваш шестикутник! Виміряйте кути транспортиром: кожен внутрішній кут має бути близьким до 120°.
- Використання транспортира. Якщо у вас є готовий шестикутник (наприклад, намальований або вирізаний із паперу), прикладіть транспортир до кожної вершини та виміряйте кут. Для правильного шестикутника результати будуть приблизно 120°.
- Програмне забезпечення. Використовуйте геометричні програми, як-от GeoGebra. Побудуйте правильний шестикутник і виміряйте його кути — програма підтвердить, що кожен кут дорівнює 120°.
Ці методи не лише підтверджують теоретичні розрахунки, але й роблять геометрію живою та захопливою. Спробуйте самі — це як відкрити маленький математичний скарб!
Типові помилки при розрахунку внутрішнього кута
Навіть у такій, здавалося б, простій темі, як внутрішні кути шестикутника, можна припуститися помилок. Ось найпоширеніші з них і як їх уникнути.
- Плутанина з зовнішніми кутами. Деякі плутають внутрішні кути із зовнішніми. Для правильного шестикутника зовнішній кут дорівнює 360° / 6 = 60°. Завжди уточнюйте, про який кут ідеться.
- Неправильне застосування формули. Іноді забувають відняти 2 від кількості сторін або не ділять суму на кількість кутів. Перевіряйте кожен крок: (6-2) × 180° / 6.
- Припущення, що всі шестикутники однакові. Внутрішній кут 120° стосується лише правильного шестикутника. У неправильному шестикутнику кути можуть бути різними.
Уважність і чітке розуміння термінів допоможуть уникнути цих пасток. Якщо сумніваєтеся, завжди повертайтеся до формули або геометричної побудови.
Застосування шестикутників у реальному світі
Знання про внутрішній кут шестикутника — це не просто абстрактна математика. Ця інформація має практичне застосування в багатьох сферах. Ось кілька прикладів, які показують, як шестикутники та їхні кути змінюють світ.
- Архітектура. Шестикутні форми використовуються в дизайні будівель і мостів завдяки їхній міцності та здатності рівномірно розподіляти навантаження. Внутрішній кут 120° забезпечує стабільність конструкцій.
- Дизайн. Шестикутні плитки та мозаїки популярні в інтер’єрах, адже вони створюють гармонійний і сучасний вигляд. Розуміння кутів допомагає дизайнерам створювати ідеальні візерунки.
- Технології. У комп’ютерній графіці та геймдизайні шестикутні сітки використовуються для створення карт і ландшафтів, адже вони забезпечують плавніші переходи, ніж квадратні сітки.
Шестикутник із його 120-градусними кутами — це справжній герой геометрії, який поєднує красу, функціональність і ефективність. Наступного разу, коли побачите шестикутну плитку чи бджолині стільники, згадайте, як математика творить дива!