Уявіть собі ідеальну форму, де кожна сторона гармонійно повторює іншу, а кути створюють бездоганну симетрію. Квадрат — це не просто геометрична фігура, а символ порядку, балансу та математичної краси. Але чому дорівнює його площа? Це питання, яке здається простим, ховає в собі глибину, що захоплює як новачків, так і просунутих любителів математики. У цій статті ми розкриємо всі аспекти обчислення площі квадрата, зануримося в його формули, розберемо приклади з реального життя та поділимося цікавинками, які здивують навіть тих, хто вважає себе експертом. Готові? Тоді давайте вирушимо в цю геометричну подорож!
Що таке квадрат і чому його площа важлива?
Квадрат — це чотирикутник із рівними сторонами та прямими кутами (90°). Його унікальність у простоті: всі сторони мають однакову довжину, а кути ідеально вивірені. Площа квадрата — це міра поверхні, яку він займає у двовимірному просторі. Вона вимірюється в квадратних одиницях (см², м², км²) і є ключем до вирішення безлічі практичних завдань.
Чому це важливо? Площа квадрата лежить в основі багатьох обчислень: від планування земельних ділянок до створення цифрових зображень. Уявіть, що ви дизайнер, який працює над піксельною сіткою, або фермер, який розраховує площу поля. Без знання площі квадрата ці задачі стають неможливими. Ця базова концепція також є фундаментом для розуміння складніших фігур, таких як прямокутники, куби чи навіть фрактали.
Формула площі квадрата: простота, що вражає
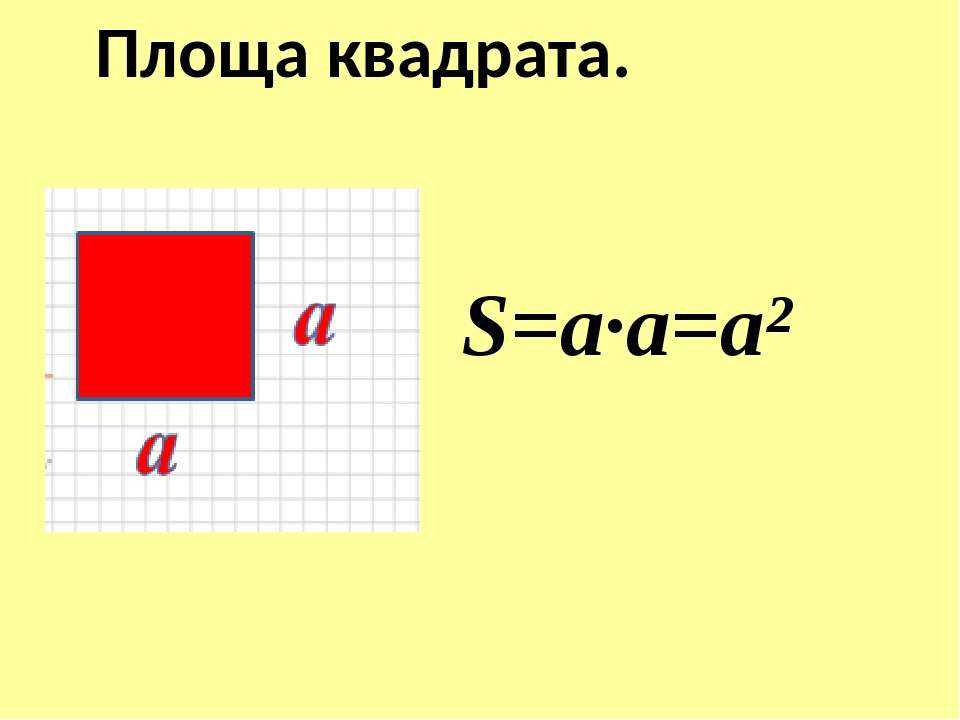
Формула площі квадрата — це, мабуть, одна з найелегантніших у математиці: S = a², де S — площа, а a — довжина сторони. Її геніальність у тому, що вона працює для будь-якого квадрата, незалежно від його розміру — від мікроскопічного пікселя до величезної площі. Але за цією простотою ховається глибокий сенс.
Чому саме квадрат сторони? Уявіть квадрат як сітку з маленьких одиничних квадратів. Якщо сторона дорівнює 3 см, то квадрат можна розбити на 3×3 = 9 маленьких квадратів, кожен із площею 1 см². Таким чином, множення сторони на себе відображає загальну кількість таких одиниць. Ця ідея настільки інтуїтивна, що навіть діти в початковій школі швидко її засвоюють, але водночас вона відкриває двері до складніших математичних концепцій.
Як працює формула: покроковий алгоритм
Обчислити площу квадрата надзвичайно легко, якщо знати послідовність дій. Ось як це зробити:
- Виміряйте довжину сторони. Використовуйте лінійку, рулетку або цифрові інструменти. Наприклад, якщо сторона квадрата — 6 см, запишіть a = 6 см.
- Возведіть сторону в квадрат. Помножте довжину сторони саму на себе: 6 × 6 = 36 см².
- Перевірте одиниці вимірювання. Якщо сторона в сантиметрах, площа буде в квадратних сантиметрах. Для метрів — у квадратних метрах.
- Перевірте точність. Якщо сторона дробова (наприклад, 2.5 см), обчислення будуть такими: 2.5 × 2.5 = 6.25 см².
Ці кроки здаються елементарними, але уважність — ключ до успіху. Наприклад, помилка в вимірюванні сторони на 1 мм може значно змінити результат для великих площ, таких як земельні ділянки. Тож завжди перевіряйте свої вимірювання!
Альтернативні способи обчислення площі квадрата
Хоча формула S = a² є найпростішою, існують інші способи знайти площу квадрата, якщо відома не сторона, а, наприклад, діагональ чи периметр. Давайте розберемо ці методи детально.
Площа через діагональ
Діагональ квадрата — це лінія, що з’єднує його протилежні кути. Її довжину можна використати для обчислення площі за формулою: S = d²/2, де d — довжина діагоналі.
Чому це працює? Діагональ квадрата пов’язана зі стороною через теорему Піфагора: d = a√2. Якщо вивести сторону з цього рівняння (a = d/√2) і підставити в основну формулу площі, отримаємо S = (d/√2)² = d²/2. Наприклад, якщо діагональ квадрата дорівнює 8 см, то:
- Обчислюємо: S = 8²/2 = 64/2 = 32 см².
- Відповідь: площа дорівнює 32 см².
Цей метод корисний, коли сторона невідома, але діагональ виміряна, наприклад, у будівництві чи дизайні.
Площа через периметр
Периметр квадрата — це сума всіх його сторін: P = 4a. Якщо відомий периметр, можна знайти сторону: a = P/4, а потім обчислити площу за основною формулою: S = (P/4)². Наприклад, якщо периметр квадрата — 20 см:
- Знаходимо сторону: a = 20/4 = 5 см.
- Обчислюємо площу: S = 5² = 25 см².
Цей спосіб зручний, коли ви маєте дані про загальну довжину сторін, наприклад, при розрахунку огорожі для квадратної ділянки.
Площа через радіус вписаного або описаного кола
Квадрат може бути вписаним у коло або мати вписане коло. Якщо відомий радіус вписаного кола (r), площу можна обчислити за формулою: S = 4r². Для радіуса описаного кола (R): S = 2R².
Ці формули менш поширені, але корисні в задачах, пов’язаних із геометричними побудовами. Наприклад, якщо радіус вписаного кола дорівнює 3 см:
- Обчислюємо: S = 4 × 3² = 4 × 9 = 36 см².
Такі методи часто застосовуються в комп’ютерній графіці чи архітектурному проєктуванні.
Практичні приклади: як площа квадрата оживає в реальному світі
Теорія — це чудово, але давайте подивимося, як обчислення площі квадрата працює в реальному житті. Ось три приклади, які покажуть, як ця формула допомагає вирішувати практичні завдання.
Приклад 1: Плитка для підлоги
Уявіть, що ви ремонтуєте кухню, і підлога має форму квадрата зі стороною 4 м. Скільки плитки потрібно? Обчислимо площу: S = 4² = 16 м². Якщо одна плитка має розмір 50×50 см (0.25 м²), то кількість плиток: 16 ÷ 0.25 = 64 плитки. Цей розрахунок допомагає точно оцінити витрати на матеріали, заощадивши ваш бюджет.
Приклад 2: Піксельна сітка в дизайні
У цифровій графіці квадратна сітка пікселів — основа зображень. Якщо кожен піксель — це квадрат 1×1 мм, а сітка має сторону 200 пікселів, то площа зображення: S = 200² = 40 000 пікселів. Це знання допомагає дизайнерам оцінити роздільну здатність і розмір файлу.
Приклад 3: Земельна ділянка
Фермер планує засіяти квадратну ділянку зі стороною 100 м. Площа: S = 100² = 10 000 м², або 1 гектар. Це дозволяє оцінити кількість насіння чи добрив, необхідних для посіву.
Ці приклади демонструють, як формула площі квадрата стає універсальним інструментом у різних сферах — від будівництва до технологій.
Одиниці вимірювання: як не заплутатися
Площа квадрата завжди вимірюється в квадратних одиницях, але важливо правильно конвертувати їх. Якщо сторона в сантиметрах, площа буде в квадратних сантиметрах. Якщо в метрах — у квадратних метрах. Ось таблиця для конвертації найпоширеніших одиниць:
| Одиниця вимірювання | Конвертація в квадратні метри |
|---|---|
| Квадратний сантиметр (см²) | 1 см² = 0.0001 м² |
| Квадратний дециметр (дм²) | 1 дм² = 0.01 м² |
| Квадратний метр (м²) | 1 м² = 1 м² |
| Гектар (га) | 1 га = 10 000 м² |
Джерело: математичні стандарти, опубліковані в навчальних посібниках з геометрії.
Щоб уникнути помилок, завжди приводьте одиниці до однієї системи перед обчисленнями. Наприклад, якщо сторона 2 м, то площа 4 м². Але якщо перевести в сантиметри (2 м = 200 см), то 200 × 200 = 40 000 см². Обидва результати правильні, але їх потрібно зіставляти коректно.
Типові помилки при обчисленні площі квадрата
Навіть найпростіша формула може стати пасткою, якщо не бути уважним. Ось найпоширеніші помилки, які допускають як новачки, так і досвідчені користувачі, і як їх уникнути.
- ❌ Неправильні одиниці вимірювання. Якщо сторона в сантиметрах, а ви обчислюєте в метрах без конвертації, результат буде хибним. Наприклад, для сторони 100 см площа — 10 000 см², а не 100 м².
- ⚠️ Плутанина з периметром. Деякі помилково додають сторони (4a) замість множення (a²). Пам’ятайте: периметр — це 4 × a, а площа — a².
- 🔍 Неточні вимірювання. Якщо сторона виміряна приблизно (наприклад, 5.1 см замість 5.12 см), це може значно вплинути на площу великих об’єктів.
- 📏 Помилки з дробами. Для сторони 3.2 см правильна площа — 10.24 см², але деякі забувають коректно множити дробові числа.
Щоб уникнути цих пасток, завжди перевіряйте одиниці, використовуйте калькулятор для дробових чисел і переконайтеся, що застосовуєте правильну формулу. Уважність — ваш найкращий союзник!
Похідні формули: зв’язок із іншими величинами
Площа квадрата — це не ізольована концепція, а частина ширшої геометричної системи. Вона пов’язана з іншими характеристиками квадрата, такими як периметр, діагональ чи об’єм куба. Ось як це працює:
- Периметр. Периметр квадрата: P = 4a. Якщо відома площа, сторону можна знайти як a = √S, а потім обчислити периметр.
- Діагональ. Діагональ обчислюється за формулою: d = a√2. Якщо відома площа, то a = √S, і діагональ буде d = √S × √2.
- Об’єм куба. Якщо квадрат є основою куба, об’єм куба: V = a³. Знаючи площу основи, можна знайти сторону (a = √S) і піднести її до куба.
Ці зв’язки показують, як площу квадрата можна використовувати для складніших обчислень, наприклад, у проєктуванні будівель чи 3D-моделюванні.
Застосування площі квадрата в реальному світі
Площа квадрата — це не просто абстрактна величина, а інструмент, який пронизує наше життя. Ось кілька сфер, де вона незамінна:
- Архітектура. Розрахунок площі квадратних плит чи вікон допомагає оптимізувати витрати матеріалів.
- Програмування. У комп’ютерній графіці квадрати використовуються для створення піксельних сіток чи ігрових рівнів.
- Сільське господарство. Фермери розраховують площу квадратних ділянок для планування посівів чи зрошення.
- Мистецтво. Квадратні полотна чи композиції створюють гармонійні візуальні ефекти.
Ці приклади показують, що знання площі квадрата — це не лише шкільна вправа, а й практичний навик, який економить час і ресурси.
Квадрат у культурі та історії
Квадрат — це не лише математична фігура, а й символ, що пронизує культуру та історію. У Стародавній Греції квадрат асоціювався з гармонією та досконалістю. Піфагорійці вважали його символом рівноваги, адже всі сторони та кути рівні. У мистецтві квадрат став знаковим завдяки Казимиру Малевичу, чий «Чорний квадрат» (1915) перевернув уявлення про абстракціонізм.
У природі квадратні форми рідкісні, але їх можна знайти в кристалах солі чи мінералах, де молекули утворюють квадратні решітки. Ця природна геометрія надихає вчених і дизайнерів, показуючи, що математика — це мова Всесвіту.
Поради для новачків і просунутих користувачів
Чи ви школяр, який тільки відкриває геометрію, чи досвідчений інженер, ці поради допоможуть вам опанувати обчислення площі квадрата:
- Завжди перевіряйте одиниці вимірювання. Переконайтеся, що всі значення в одній системі, щоб уникнути помилок.
- Використовуйте калькулятор для дробів. Це особливо важливо для складних чисел, наприклад, 7.83 см.
- Візуалізуйте задачу. Намалюйте квадрат на папері або уявіть його як сітку одиничних квадратів — це спрощує розуміння.
- Експериментуйте з альтернативними формулами. Спробуйте обчислити площу через діагональ чи периметр, щоб поглибити розуміння.
Ці поради допоможуть вам не лише правильно обчислити площу, а й відчути радість від роботи з геометрією.
Як перевірити правильність обчислень?
Щоб переконатися, що ваша площа обчислена правильно, виконайте ці кроки:
- Перевірте вимірювання. Переміряйте сторону чи діагональ, щоб виключити помилки.
- Використовуйте альтернативний метод. Наприклад, якщо ви обчислили площу через сторону, перевірте через діагональ.
- Порівняйте з реальними даними. Якщо це земельна ділянка, оцініть, чи відповідає результат вашим очікуванням (наприклад, 10 000 м² = 1 га).
Ці методи гарантують точність і впевненість у ваших обчисленнях.
Квадрат у шкільній освіті
Площа квадрата — одна з перших тем, яку діти вивчають у школі, зазвичай у 2–3 класі. Вона допомагає розвинути просторове мислення, розуміння одиниць вимірювання та вміння аналізувати. У старших класах квадрат стає основою для вивчення складніших фігур, таких як ромби чи паралелограми.
Учителі часто використовують практичні завдання, наприклад, обчислення площі квадратного аркуша паперу чи плитки, щоб зробити тему цікавою. Це не просто математика — це спосіб показати дітям, як геометрія оживає в реальному світі.
Квадрат — це більше, ніж просто фігура. Це ключ до розуміння симетрії, гармонії та практичних рішень у нашому житті. Відкрийте для себе його магію, і ви побачите, як математика стає захопливою пригодою!