Площа трикутника – це не просто число, яке ми обчислюємо на уроках геометрії. Це ключ до розуміння простору, форм і навіть природи навколо нас. Уявіть трикутник як маленьку сцену, де розгортаються великі математичні історії: від будівництва пірамід до створення 3D-моделей у комп’ютерних іграх. У цій статті ми розберемо, як знайти площу трикутника, розглянемо всі можливі формули, розкриємо їхню магію та поділимося практичними прикладами.
Що таке площа трикутника і чому вона важлива
Трикутник – це найпростіша замкнена геометрична фігура, утворена трьома відрізками, що з’єднують три точки, які не лежать на одній прямій. Площа трикутника – це чисельна характеристика, яка показує, скільки простору займає ця фігура на площині. Вона вимірюється в квадратних одиницях: сантиметрах, метрах чи навіть кілометрах.
Чому це важливо? Площа трикутника – це основа для багатьох практичних задач. Архітектори використовують її, щоб розрахувати кількість матеріалів для трикутного даху. Дизайнери одягу обчислюють площу тканини для викрійок. Навіть у природі трикутники всюди: від структури листя до кристалічних решіток. Розуміння, як знайти площу, відкриває двері до вирішення реальних проблем.
Основні формули для обчислення площі трикутника
Існує безліч способів знайти площу трикутника, і кожен із них – як окремий ключ до однієї скрині. Вибір формули залежить від того, які дані у вас є: сторони, висота, кути чи навіть координати вершин. Розглянемо найпоширеніші методи.
1. Класична формула: основа та висота
Найпростіший і найвідоміший спосіб обчислити площу трикутника – це використати його основу та висоту. Основа – це будь-яка сторона трикутника, а висота – перпендикуляр, опущений із протилежної вершини до цієї основи.
Формула: S = ½ × a × h
- a – довжина основи.
- h – висота, проведена до основи.
Приклад: Уявімо трикутник із основою 8 см і висотою 5 см. Підставимо в формулу:
S = ½ × 8 × 5 = 20 см²
Цей метод ідеальний, коли висота відома або її легко знайти. Наприклад, у прямокутному трикутнику один катет може бути основою, а другий – висотою. Але що робити, якщо висота не дана? Тоді на допомогу приходять інші формули.
2. Через дві сторони та кут між ними
Якщо ви знаєте довжини двох сторін трикутника та кут між ними, тригонометрія стане вашим найкращим другом. Ця формула використовує синус кута, що робить її особливо зручною для нестандартних трикутників.
Формула: S = ½ × a × b × sin(C)
- a, b – довжини двох сторін.
- C – кут між цими сторонами.
Приклад: У трикутнику сторони 6 см і 7 см, а кут між ними – 45°. Обчислимо:
S = ½ × 6 × 7 × sin(45°) ≈ ½ × 6 × 7 × 0,707 ≈ 14,85 см²
Цей метод зручний, коли ви працюєте з тригонометричними задачами або маєте дані про кути. Наприклад, синус 45° дорівнює приблизно 0,707, що спрощує обчислення.
3. Формула Герона: через три сторони
Формула Герона – це справжня перлина для тих, хто знає лише довжини трьох сторін трикутника. Вона дозволяє знайти площу без висоти чи кутів, що робить її універсальною.
Формула: S = √(p × (p – a) × (p – b) × (p – c))
- a, b, c – довжини сторін.
- p – напівпериметр: p = (a + b + c) / 2.
Приклад: Сторони трикутника – 3 см, 4 см і 5 см. Знайдемо напівпериметр:
p = (3 + 4 + 5) / 2 = 6
Тепер підставимо в формулу:
S = √(6 × (6 – 3) × (6 – 4) × (6 – 5)) = √(6 × 3 × 2 × 1) = √36 = 6 см²
Формула Герона ідеально підходить для будь-яких трикутників, особливо якщо вони нерегулярні. Але не забудьте перевірити нерівність трикутника: сума будь-яких двох сторін має бути більшою за третю.
4. Для прямокутного трикутника
Прямокутні трикутники – це математичний подарунок, адже їхня структура спрощує обчислення. Площу можна знайти через два катети, які утворюють прямий кут.
Формула: S = ½ × a × b
- a, b – довжини катетів.
Приклад: Катети трикутника – 3 см і 4 см. Тоді:
S = ½ × 3 × 4 = 6 см²
Цей метод працює, тому що один катет є основою, а другий – висотою. Це найшвидший спосіб для прямокутних трикутників.
5. Через координати вершин
Якщо трикутник заданий координатами його вершин на площині, можна скористатися методом із векторної алгебри. Це звучить складно, але насправді це просто формула, яка працює як магія.
Формула: S = ½ × |(x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂))|
- (x₁, y₁), (x₂, y₂), (x₃, y₃) – координати вершин.
Приклад: Вершини трикутника: A(0, 0), B(4, 0), C(0, 3). Підставимо:
S = ½ × |(0 × (0 – 3) + 4 × (3 – 0) + 0 × (0 – 0))| = ½ × |12| = 6 одиниць²
Цей метод ідеальний для аналітичної геометрії чи комп’ютерної графіки, де трикутники часто задають координатами.
Спеціальні випадки: рівносторонні та рівнобедрені трикутники
Деякі трикутники мають особливі властивості, які дозволяють використовувати спрощені формули. Розглянемо два найпоширеніші типи.
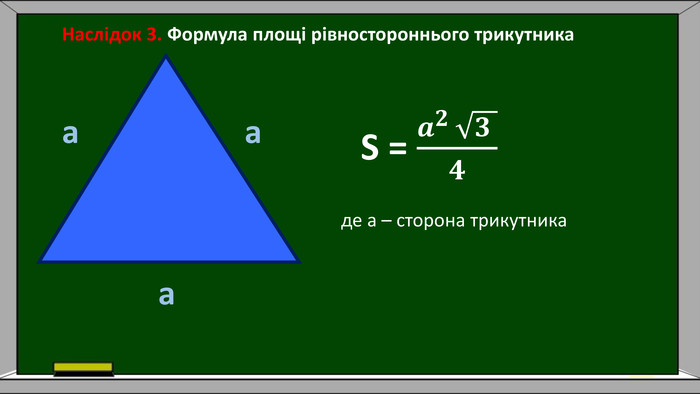
Рівносторонній трикутник
У рівносторонньому трикутнику всі сторони та кути рівні (кути по 60°). Це дозволяє обчислити площу через одну сторону.
Формула: S = (√3 × a²) / 4
- a – довжина сторони.
Приклад: Сторона трикутника – 4 см. Тоді:
S = (√3 × 4²) / 4 = (√3 × 16) / 4 ≈ 6,93 см²
Ця формула зручна, адже не потрібно знати висоту чи кути – лише довжину сторони.
Рівнобедрений трикутник
У рівнобедреному трикутнику дві сторони рівні, що спрощує обчислення. Площу можна знайти через основу та бічну сторону.
Формула: S = (b / 4) × √(4a² – b²)
- a – бічна сторона.
- b – основа.
Приклад: Основа – 6 см, бічна сторона – 5 см. Тоді:
S = (6 / 4) × √(4 × 5² – 6²) = 1,5 × √(100 – 36) = 1,5 × √64 = 12 см²
Ця формула дозволяє обійтися без висоти, що зручно для рівнобедрених трикутників.
Практичні приклади для закріплення
Щоб формули стали частиною вашого арсеналу, розглянемо кілька практичних задач.
- Задача 1: Основа та висота. Основа трикутника – 10 м, висота – 7 м. Знайдіть площу.
- Задача 2: Формула Герона. Сторони трикутника – 5 см, 6 см, 7 см. Знайдіть площу.
- Задача 3: Дві сторони та кут. Сторони 8 см і 9 см, кут між ними – 60°. Знайдіть площу.
Ці приклади показують, як різні формули можуть привести до однієї відповіді. Спробуйте накреслити трикутник на папері – це допоможе візуалізувати задачу.
Типові помилки при обчисленні площі трикутника
Обчислення площі трикутника здається простим, але навіть досвідчені математики можуть зробити помилку. Ось найпоширеніші пастки та як їх уникнути.
- 🚫 Неправильні одиниці вимірювання. Якщо одна сторона в метрах, а інша в сантиметрах, результат буде хибним. Завжди переводьте всі дані в одну систему.
- ⚠️ Плутанина з висотою. Висота – це перпендикуляр до основи, а не будь-яка лінія. Переконайтеся, що ви правильно визначили висоту.
- ❌ Порушення нерівності трикутника. Перевірте, чи сума двох сторін більша за третю. Наприклад, трикутник із сторонами 1, 1 і 3 не існує.
- 🔍 Помилка в обчисленнях синусів. При використанні формули з синусом переконайтеся, що кут у градусах, а не в радіанах.
Ці помилки легко уникнути, якщо бути уважним і перевіряти дані перед обчисленнями. Завжди округляйте лише в кінці, щоб зберегти точність.
Порівняння методів: який обрати?
Кожен метод обчислення площі має свої сильні сторони. Ось таблиця, яка допоможе вибрати найкращий спосіб залежно від даних.
| Метод | Що потрібно | Коли використовувати |
|---|---|---|
| Основа та висота | Основа, висота | Найпростіший метод, якщо висота відома. |
| Дві сторони та кут | Дві сторони, кут між ними | Для тригонометричних задач. |
| Формула Герона | Три сторони | Коли відомі лише сторони. |
| Прямокутний трикутник | Два катети | Для прямокутних трикутників. |
| Координати вершин | Координати трьох точок | Для аналітичної геометрії. |
Джерела: LibreTexts, znai.com.ua
Вибір методу залежить від вихідних даних. Якщо ви не впевнені, почніть із найпростішого – основи та висоти – і поступово переходьте до складніших формул.
Цікаві факти про площу трикутника
Трикутники – це не лише формули, а й захоплюючі історії, які пов’язують математику з реальним світом. Ось кілька цікавих фактів, які додадуть вам любові до цієї геометричної фігури.
- 📐 Трикутник – найміцніша фігура. Завдяки своїй структурі трикутники не деформуються під тиском, тому їх використовують у конструкціях мостів, веж і навіть космічних кораблів.
- 🕰️ Формула Герона старша за нас. Її відкрив Архімед ще в III столітті до н.е., але назвали на честь Герона Александрійського, який популяризував її в I столітті н.е.
- 🌍 Трикутники в природі. Від структури молекул води до форми сніжинок – трикутники всюди в природі, а їхня площа допомагає вченим аналізувати ці структури.
- 🎮 Трикутники в іграх. У комп’ютерній графіці 3D-об’єкти розбиваються на тисячі трикутників, а їхня площа визначає, як об’єкт виглядатиме на екрані.
Ці факти показують, що трикутники – це не просто шкільна математика, а основа багатьох аспектів нашого життя. Спробуйте знайти трикутники навколо себе – ви здивуєтеся, як часто вони трапляються!
Як застосувати знання в реальному житті
Обчислення площі трикутника – це не лише для контрольних робіт. Ось як ці знання можуть стати в пригоді:
- Будівництво. Розрахуйте площу трикутного фронтону даху, щоб визначити, скільки черепиці потрібно.
- Дизайн. Визначте, скільки тканини потрібно для трикутного вітрила чи штори.
- Садівництво. Обчисліть площу трикутної клумби, щоб знати, скільки ґрунту закупити.
- Комп’ютерна графіка. Площа трикутників лежить в основі 3D-моделювання, де кожен об’єкт складається з безлічі трикутників.
Завжди перевіряйте, чи ваш результат має сенс. Наприклад, якщо ви отримали площу 100 м² для трикутника зі стороною 2 см, щось пішло не так. Перевірте одиниці вимірювання та формулу.
Трикутники – це маленькі будівельні блоки великого світу математики. Зрозумівши, як знайти їхню площу, ви відкриваєте двері до безлічі практичних і творчих застосувань.